RHÉOLOGIE

RHÉOLOGIE

Le mot «rhéologie» (du grec: 福﨎晴益, s’écouler) a été proposé par Eugene Cook Bingham, en 1928, pour désigner «la science qui étudie les déformations et l’écoulement de la matière». Plus exactement, l’objet de la rhéologie est l’étude du comportement mécanique, c’est-à-dire des relations entre les déformations et les contraintes de la matière. Ensuite, s’appuyant sur la connaissance de ce comportement, on calculera, grâce à la mécanique des milieux continus, la répartition non uniforme des contraintes et des déformations dans un corps sous l’effet des forces extérieures. Dans ses calculs pratiques, l’ingénieur fait appel aux disciplines appliquées, telles la résistance des matériaux et l’hydraulique.

En réalité, la rhéologie a été créée pour répondre aux besoins de la technologie moderne; les différentes branches de la mécanique développées au XIX^e siècle (l’élasticité, la plasticité, la mécanique des fluides) ne sont fondées que sur certains schémas simples de comportement (cf. chap. 2), schémas quelquefois insuffisants pour décrire fidèlement les réponses de la matière réelle. Or, les techniciens qui étudient la transformation des matériaux, leur emploi ou simplement leur transport dans des conduites ont besoin de connaître aussi exactement que possible leurs propriétés mécaniques. Cela explique pourquoi la rhéologie, en tant que discipline, s’intéresse à un éventail considérable de corps: métaux et alliages, plastiques et caoutchoucs, produits pétroliers (bitumes, asphaltes, huiles), sols (sables, argiles, boues), roches (naturelles et artificielles), verres, bois, peintures, mastics, encres d’imprimerie, colles, crèmes pharmaceutiques et cosmétiques, produits alimentaires, substances biologiques.

Les études en rhéologie se situent sur trois voies: il y a d’abord la recherche expérimentale sur les matériaux réels, puis l’étude théorique des diverses formes de lois de comportement (étude macroscopique), enfin, l’influence de la structure de la matière sur ce comportement: molécules, réseau cristallin, grains (étude microscopique).

1. Généralités

L’expérience quotidienne suggère de distinguer les solides des fluides (liquides et gaz). En principe, le fluide soumis à une pression hydrostatique ne se déforme que d’une quantité finie, tandis qu’une contrainte de cisaillement (cission), même faible, provoque un écoulement indéfini. La déformation d’un solide, au contraire, reste finie dans les deux cas, pourvu que la cission ne dépasse pas un certain seuil.

Cette distinction perd souvent son sens en rhéologie: les matériaux réels se situent fréquemment entre ces deux cas extrêmes, et il est préférable de parler de corps peu déformables (solides au sens habituel) et de corps très déformables (fluides).

Le comportement du même matériau peut être différent selon les conditions de travail: niveau des contraintes, vitesse de charge, durées de sollicitation ou du repos, température, etc. C’est ainsi que l’acier peut présenter, selon les cas, des caractères prépondérants d’élasticité, de viscosité ou de plasticité. Les roches, élastiques-fragiles sous pression atmosphérique, peuvent subir de très fortes déformations plastiques sous haute pression (cf. photo). Les apparences peuvent aussi différer selon les circonstances. À la température ambiante, le brai (résidu de la distillation du goudron) semble solide et cassant pour les essais rapides, mais il coule, à la longue, sur une paroi verticale. La description d’un comportement comprend, ne serait-ce qu’implicitement, les limites de sa validité. L’étude de ces limites: seuil d’écoulement, rupture, fatigue, changements d’état, etc., appartient ainsi au domaine de la rhéologie.

Enfin, les phénomènes mécaniques et thermiques sont intimement liés; chaque déformation est accompagnée de processus thermiques ^{[cf. THERMODYNAMIQUE]}. Les bases thermodynamiques des lois de comportement sont établies d’une manière plus ou moins satisfaisante. Pour simplifier l’exposé, on supposera que les expériences sont faites à température constante.

2. Principaux comportements

Pour donner une description mathématique précise du comportement mécanique macroscopique observé, on suppose que toutes les grandeurs qui caractérisent la réponse de la matière sont réparties d’une manière continue. Une telle conception, qui repose sur certaines hypothèses statistiques implicites, permet de définir la distribution des déformations et des contraintes comme des champs tensoriels (cf. ÉLASTICITÉ, mécanique des FLUIDES). Les relations entre ces champs sont appelées lois de comportement ou équations constitutives.

En rhéologie, pour englober toute la variété des propriétés des matériaux réels, on se sert souvent de la description à un paramètre, où une contrainte représentative est reliée à la déformation ou à la vitesse de déformation correspondantes. Pour fixer les idées, cette contrainte peut être une traction ou une cission pour les corps peu déformables; elle est de préférence une cission pour les corps très déformables. La généralisation au milieu tridimensionnel ne pose en général que des difficultés d’ordre mathématique.

Comportements élémentaires

Un solide idéal qui ne se déformerait pas, même sous l’action de forces élevées, est appelé solide d’Euclide, tandis que le solide de Hooke se déforme linéairement avec la contrainte ^{[cf. ÉLASTICITÉ]}. Dans les schémas rhéologiques, ce dernier se représente par un ressort (fig. 1 a). Un autre solide idéal, représenté par un patin (fig. 1 b), est qualifié de rigide-plastique. Soumis à une contrainte de cisaillement, il ne se déforme qu’à partir d’un certain seuil que la contrainte ne peut en aucun cas dépasser.

Si le liquide de Pascal, parfaitement mobile et incompressible, n’oppose que son inertie à la déformation de cisaillement, le liquide de Newton est caractérisé par une proportionnalité entre la contrainte et la vitesse de déformation. Il est représenté par un amortisseur (fig. 1 c).

Ces trois sortes de propriétés sont ensuite associées pour représenter de nombreux comportements réels. Néanmoins, certains de ceux-ci échappent à ce mode de représentation et nécessiteraient l’introduction d’autres modèles élémentaires.

Viscoélasticité

Ce sont principalement les hauts polymères (par exemple poly-isobutylène sec ou en solution) qui manifestent de la viscoélasticité; mais divers autres matériaux en sont doués aussi: pâtes boulangères, argiles, etc.

Ce phénomène apparaît nettement au cours d’un essai de relaxation ou d’un essai de retard (appelé quelquefois essai de fluage ; cf. MÉTALLOGRAPHIE – Essais mécaniques). Dans l’essai de relaxation (fig. 2), une déformation est imposée brusquement, puis maintenue constante ensuite. La contrainte qui en résulte diminue progressivement à mesure que le temps s’écoule. Dans le second type d’essai (fig. 3), qui s’applique aussi bien aux solides qu’aux liquides, c’est la contrainte qui est appliquée brusquement et maintenue constante pendant un certain temps. À la déformation élastique instantanée s’ajoute une déformation différée (ou retardée). La suppression brusque de la contrainte (décharge) entraîne de la même façon une recouvrance élastique instantanée suivie d’une recouvrance différée, de nature viscoélastique. Le fluage est, pour les métallurgistes, une déformation retardée non recouvrable à la décharge.

Linéarité du comportement

Les expressions qui suivent sont générales pour un processus unidimensionnel. Les rapports qui y sont définis (fonction de relaxation, fonction de retard, modules, complaisances, coefficients de viscosité, etc.) ne correspondent quelquefois à ceux, usuels, de la théorie tridimensionnelle qu’à un facteur près.

Une frontière importante est à jeter entre les comportements dits linéaires et ceux qui ne le sont pas. Boltzmann, en 1874, a posé le principe de superposition qui porte son nom et qui peut servir de base à la linéarité. La contrainte supportée par un corps à un instant donné ne dépend pas seulement de la déformation actuelle du corps, mais aussi des déformations qu’il a subies dans le passé. Cette contrainte est la somme de toutes celles que chacune de ces déformations aurait produites à l’instant actuel si elle avait agi seule. En prenant comme origine des temps l’instant de la première sollicitation, ou un instant antérieur, cette additivité des effets des actions passées et actuelle se traduit par la relation:

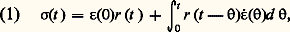où 靖 est la contrainte, 﨎 la déformation, 﨎 la vitesse de déformation et où r (t ) est appelée fonction de relaxation. En effet, au cours d’une expérience de relaxation, la déformation constante étant imposée à partir de l’instant t = 0 (fig. 2), la relation (1) se réduit à:

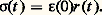Des explications identiques peuvent être données en permutant les mots «déformation» et «contrainte». La relation homologue à (1) s’écrit:

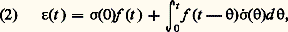où 靖 est la dérivée de la contrainte par rapport au temps. On appelle f (t ) fonction de retard, car une expérience de retard (fig. 3) conduit à:

En faisant intervenir les transformées de Laplace-Carson des grandeurs qui entrent en jeu, transformées désignées par les mêmes lettres surmontées d’une croix, les relations (1) et (2) deviennent:

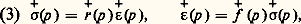où p est la variable habituelle de calcul symbolique ^{[cf. SYMBOLIQUE]}. Il est possible, si le comportement est linéaire, de calculer la fonction de retard, connaissant la fonction de relaxation, et réciproquement, puisque:

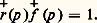Essai harmonique

L’application d’une sollicitation sinusoïdale fait apparaître un retard de la déformation sur la contrainte:

où 靖^m et 﨎^m expriment l’amplitude des oscillations, 諸 la pulsation et i le symbole des imaginaires. Cette différence de phase 﨏, appelée angle de perte, nulle pour le solide élastique de Hooke, atteint 90⁰ pour le liquide de Newton. Pour les corps viscoélastiques, elle dépend de la fréquence.

L’énergie dissipée par cycle et par unité de volume est: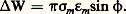

C’est l’aire du cycle d’hystérésis décrit dans le diagramme contrainte-déformation. Le rapport 靖/ 﨎 et son inverse conduisent à définir le module complexe:

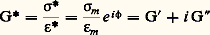et la complaisance complexe:

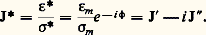Entre les composantes de ces grandeurs existent les relations suivantes:

en outre:

Le module et la complaisance complexes sont les images Laplace-Carson des fonctions de relaxation et de retard, dans lesquelles la variable p est remplacée par i 諸:

les essais harmoniques sont donc facilement reliables aux essais transitoires (relaxation et retard).

En viscoélasticité linéaire, le passage au milieu tridimensionnel n’offre pas de difficulté particulière. Les équations classiques de l’élasticité, qui sont une généralisation des équations (3), restent valables entre les images Laplace-Carson des déformations, des contraintes et des coefficients élastiques, fonctions du temps. Dans le cas particulier du régime harmonique, ce sont ces mêmes grandeurs, sous leur forme complexe (et fonction de la fréquence), qu’il est avantageux de considérer dans les équations classiques.

Modèles viscoélastiques

Un comportement viscoélastique linéaire peut se représenter par des associations de ressorts et d’amortisseurs, éventuellement en nombre infini. Les deux modèles principaux, représentés sur la figure 4, permettent de donner une forme mathématique, l’un à la fonction de relaxation: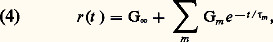

où 精^m = 兀^m /G^m est le temps de relaxation, l’autre à la fonction de retard:

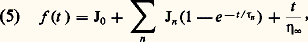où 精ⁿ = Jⁿ 兀ⁿ est le temps de retard.

On en déduit les valeurs du module complexe:

et de la complaisance complexe:

Les coefficients 兀^m , 兀ⁿ et 兀 size=1^秊 sont définis sur la figure 4.

Pour préciser davantage les propriétés des corps réels, on est amené à envisager une distribution continue des temps de relaxation et de retard. Si H( 精) d ln 精 est la somme des modules correspondant aux temps de relaxation dont les logarithmes sont compris entre ln 精 et ln 精 + d ln 精, les relations (4) et (6) deviennent: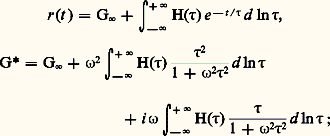

la courbe de H( 精) en fonction de ln 精 s’appelle le spectre des temps de relaxation.

Quant aux relations (5) et (7), elles deviennent, pour une distribution continue des temps de retard:

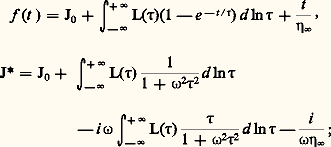la courbe de L( 精) en fonction de ln 精 s’appelle le spectre des temps de retard.

Élastoplasticité

Une pièce métallique soumise à une force supérieure à un certain niveau ne reprend pas ses dimensions primitives après retour au repos. Aux basses températures, cette déformation rémanente dépend peu de la durée de la sollicitation. C’est le phénomène d’élastoplasticité.

Le seuil de plasticité est souvent mal défini et dépend notamment de la précision avec laquelle les dimensions sont mesurées. Au-delà de ce seuil apparaissent des modifications des propriétés mécaniques, appelées écrouissage. En déformation croissante, le seuil de plasticité s’élève: c’est le durcissement. En revanche, le seuil peut s’abaisser en valeur absolue pour des contraintes du signe opposé: c’est l’effet Bauschinger. Dans une certaine mesure, il est possible de rendre compte de ces faits avec des modèles comprenant des ressorts et des patins (fig. 5). La courbe de première déformation a sa convexité tournée vers l’axe des contraintes et peut comporter des points anguleux. Si 靖 = S( 﨎) est son équation et si, à partir du point A, la sollicitation se met à décroître, la courbe de retour est donnée par:

cette homothétie de rapport 漣 2 fait apparaître l’effet Bauschinger.

Après avoir décrit cet arc jusqu’au point B (fig. 6), un nouveau changement de sens place le point représentatif sur un arc d’équation: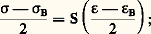

lorsque 靖^B = 0, cela rend compte du durcissement.

Ce troisième arc repasse par A. L’accommodation est immédiate. Cela veut dire que, si l’une des variables oscille entre deux limites A et B, le cycle d’hystérésis obtenu est fixé dès le premier aller et retour. Son aire représente évidemment l’énergie perdue par unité de volume.

Ce qui vient d’être dit concerne toute association entièrement décomposable en branches disposées soit en série, soit en parallèle. Lorsque les modèles font apparaître des ponts (fig. 7), les propriétés sont moins simples. L’accommodation peut être différée (fig. 8) ou supprimée complètement. Dans ce dernier cas, la déformation augmente d’une quantité constante à chaque cycle de contrainte. Lors de sollicitations triaxiales, la plasticité apparaît lorsque le déviateur des contraintes satisfait à un critère déterminé: Tresca, von Mises ou autres.

Viscoplasticité

Pour les corps plastiques réels, pour les métaux à une température notable (vis-à-vis du point de fusion), pour la pâte à modeler, le beurre à 20 ⁰C, le ciment avant la prise, etc., la contrainte nécessaire pour provoquer l’écoulement dépend de la vitesse de déformation 﨎: l’écoulement est viscoplastique.

Le cas idéal le plus simple est ceui de Bingham. L’écoulement ne se produit qu’à partir d’un certain seuil s bien défini, et il est ensuite linaire (fig. 9):

le modèle correspondant est représenté sur la figure 10.

Les associations plus compliquées de patins et d’amortisseurs sont susceptibles de reproduire tous les écoulements dépourvus d’hystérésis de vitesse de déformation (la courbe de retour coïncide avec celle d’aller dans le diagramme 靖- 﨎) et dont la viscosité apparente diminue avec la contrainte. Certains les qualifient de pseudoplastiques. Il est plus correct de les appeler fluidifiants stables (cf. infra , Corps très déformables ). Une équation souvent proposée pour des corps aussi différents que les métaux, la glace, la crème du lait est la suivante:

où k et n sont des constantes.

Corps très déformables

Les corps très déformables sont les pâtes, crèmes, peintures, solutions et dispersions diverses. L’expérience type consiste à les placer dans un viscosimètre rotatif (à plan cône ou à cylindres coaxiaux) dont la vitesse est imposée. Considérons un écoulement où, après un long repos, la vitesse de déformation est brusquement appliquée, puis maintenue constante. La viscosité apparente (rapport 靖/ 﨎) peut dépendre de cette vitesse et de la durée t d’application de cette vitesse. Il y a fluidification si, pour une durée t déterminée, la viscosité apparente est fonction décroissante de la vitesse. Il y a épaississement (certains disent dilatance) dans le cas contraire (fig. 11). Une suspension aqueuse d’amidon est épaississante. La fluidification est stable, progressive ou dégressive suivant que, lorsque la durée t augmente, la viscosité apparente reste invariable, décroît ou croît. L’épaississement est stable, progressif ou dégressif suivant que, quand la durée t augmente, la viscosité apparente reste invariable, croît ou décroît. Si ces corps sont stables, il n’y a pas d’hystérésis de vitesse de déformation. Il y a seulement viscosité anormale.

La thixotropie caractérise un matériau fluidifiant progressif qui revient à son état initial après un long repos. Il s’agit là d’un phénomène fréquent, manifesté par diverses suspensions: hydroxyde ferrique et argiles dans l’eau, peintures, etc. L’antithixotropie est la propriété, plus rare, d’un corps fluidifiant dégressif qui recouvre également son état initial après un long repos.

3. Structure et comportement

Les rhéologues se proposent d’expliquer les comportements observés à partir de la structure des corps ou, au moins, de les relier à certaines particularités physiques, physico-chimiques ou chimiques, dans l’espoir d’élaborer ensuite des matériaux possédant des propriétés mécaniques choisies à l’avance. Sans aller si loin, car leur domaine est beaucoup plus complexe, les biorhéologues établissent des corrélations avec certains états physiologiques ou pathologiques, corrélations susceptibles d’étayer ou de simplifier un diagnostic.

L’élasticité pure fait intervenir des modifications faibles, réversibles mais non uniformes des distances interatomiques. Cauchy a montré que le coefficient de Poisson ^{[cf. ÉLASTICITÉ]} serait de 0,25 si ces variations étaient uniformes. La viscosité des liquides fait appel à des déplacements irréversibles des molécules les unes par rapport aux autres (théories d’Eyring, de Mooney, etc.). La viscoplasticité des solides cristallins s’explique, dans une certaine mesure, par la théorie des dislocations ^{[cf. CRISTAUX]}. La théorie de la haute élasticité caoutchoutique après une approche thermodynamique repose sur la statistique des configurations des longues chaînes macromoléculaires, considérées comme libres entre deux nœuds (Kuhn...). Pour les polymères en général, qui, suivant la température, peuvent être vitreux (avec, quelquefois, des cristallites), caoutchoutiques ou liquides, tous les mécanismes indiqués ci-dessus interviennent.

Les dispersions constituent un monde à part. Chaque particule est entourée d’un cortège de molécules de la phase continue (couche de solvatation) et quelquefois d’une atmosphère ionique, de sorte que des actions mécaniques s’exercent entre elles à distance. Si ces actions sont de nature attractive, il peut s’établir au repos une structure (château de cartes) telle que la dispersion soit comparable à un gel. L’agitation détruit cette structure et produit une fluidification qui peut être progressive. Si, par suite du retour au repos, la reconstruction de la structure n’est pas instantanée, on a affaire à la thixotropie. Au contraire, des actions répulsives entraînent le rhéo-épaississement.

4. Mesures rhéologiques et essais industriels

Les essais en rhéologie ont pour but de définir un comportement et de déterminer les paramètres qui le caractérisent. Outre les problèmes de précision, liés aux exigences de la théorie sous-jacente à l’expérience et qui sont inhérents à toute mesure, une question essentielle soulevée par de telles expériences est celle de la pureté. Une mesure est dite pure lorsque les effets secondaires peuvent être négligés. Dans le cas contraire, il faut pouvoir les calculer.

Dans les essais dits statiques, ou dans un régime d’écoulement permanent, on tend à obtenir l’uniformité de la sollicitation dans l’espace et la constance de la température. Dans certains essais à vitesse de déformation élevée, on ne peut éviter une accélération notable des divers points matériels; dans ce cas, l’interprétation des expériences, qui repose sur la comparaison des résultats expérimentaux et théoriques, est souvent très difficile.

Les essais industriels, très fréquents dans les applications de la rhéologie, ont un rôle tout à fait différent. Il s’agit ici de l’appréciation rapide et comparative de qualité sur des échantillons selon des critères purement conventionnels (cf. MÉTALLOGRAPHIE - Essais mécaniques). En voici quelques exemples: rayage, dureté par indentation d’une bille, d’une pyramide ou d’une aiguille, emboutissage, résilience, écrasement entre deux plateaux, mouvement d’une bille dans un tube. Même si les résultats de ces expériences ne sont pas facilement exploitables pour définir les propriétés intrinsèques du matériau, le répertoire des expériences de routine joue toujours un rôle important dans la rhéologie d’un matériau spécifique.

rhéologie [ reɔlɔʒi ] n. f.

• 1943; angl. rheology (1928); de rhéo- et -logie

♦ Phys. Branche de la mécanique qui étudie le comportement des matériaux lié aux contraintes et aux déformations. Applications de la rhéologie dans l'étude de la résistance des matériaux.

● rhéologie nom féminin Science des lois du comportement des matériaux, liant, à un instant donné, les contraintes aux déformations.

rhéologie

n. f. PHYS Branche de la mécanique qui étudie les comportements de la matière sous l'influence des pressions (phénomènes d'écoulement, réactions aux contraintes, etc.).

rhéologie [ʀeɔlɔʒi] n. f.

ÉTYM. 1943; angl. rheology (1928); de rhéo-, et -logie.

❖

♦ Phys. Branche de la mécanique qui étudie le comportement de la matière en fonction de la viscosité, de l'élasticité et de la plasticité, sous le rapport des déformations et des contraintes. || Rhéologie théorique. || Applications de la rhéologie dans l'étude de la résistance des matériaux. || Rhéologie sanguine : étude dynamique de la circulation sanguine.

❖

DÉR. Rhéologique, rhéologue.

Encyclopédie Universelle. 2012.